
The main goal of this post is to detail my development of a model for doing predictive maintenance on commercial turbofan engines. The predictive maintenance method utilized here is a data-driven method, which means that data from the operating jet engine is used to simulate predictive maintenance.
The project’s goal is to develop a prediction model for estimating a jet engine’s Remaining Useful Life ( RUL) based on run-to-failure data from a fleet of comparable jet engines.
Overview of the data set
The Prognostics and Health Management PHM08 Challenge Data Set was developed by NASA and is now available to the public. The data collection is used to forecast jet engine problems over time. The Prognostics CoE at NASA Ames contributed the data set.
https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/#turbofan
The data set for the jet engine comprises time-series measurements of different pressures, temperatures, and rotating equipment speeds. In a commercial contemporary turbofan engine, these metrics are routinely taken.
Although all engines are of the same kind, each one begins with varying degrees of early wear and manufacturing process differences that are undisclosed to the user. Each machine has three alternative settings that may be utilized to alter its performance. Each engine contains 21 sensors that gather data about the engine’s status while it’s running.
Let’s make time series plots for two units, so we can get a sense of the data.
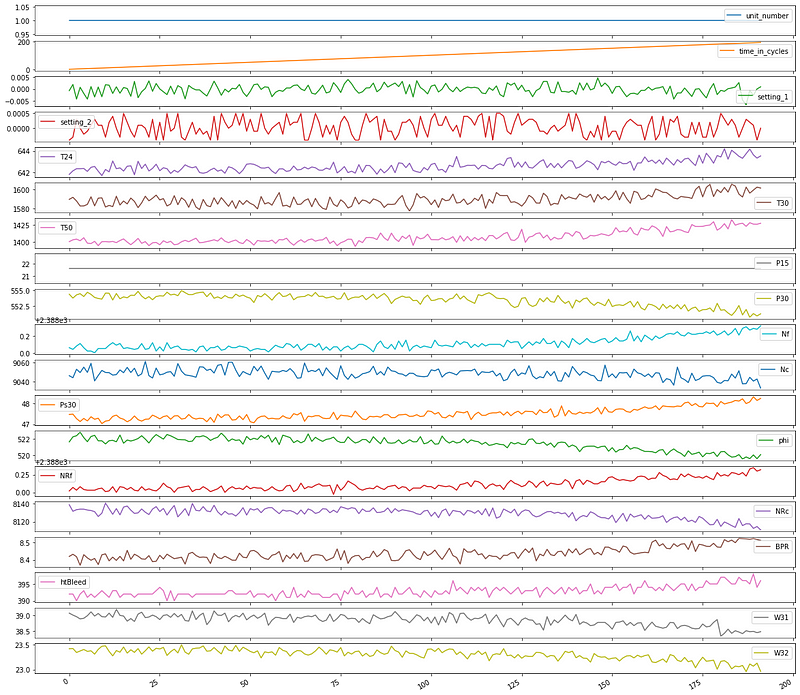
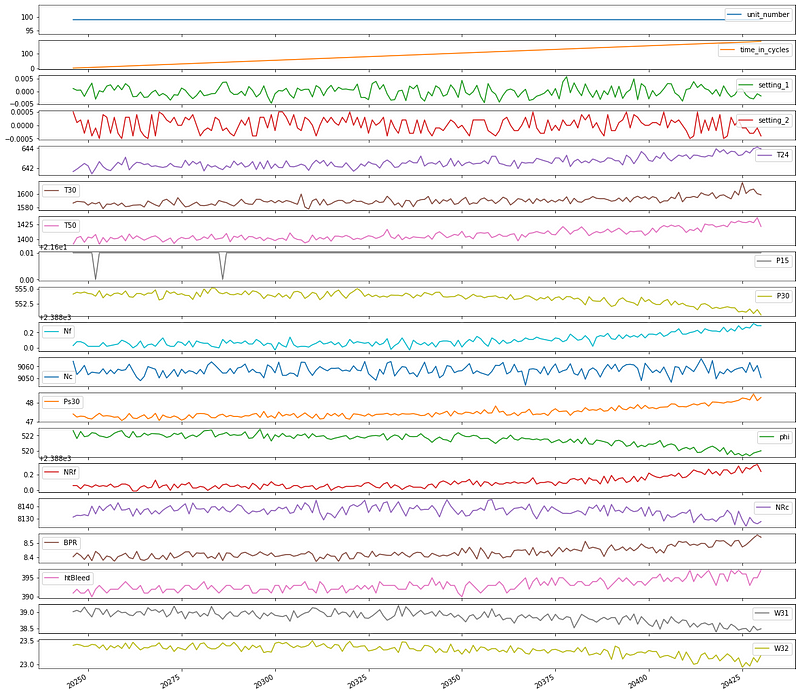
We can see that the different unit numbers have a different number of total cycles before they fail.
Let’s look at this more closely:
count 100.000000 mean 206.310000 std 46.342749 min 128.000000 25% 177.000000 50% 199.000000 75% 229.250000 max 362.000000 Name: time_in_cycles, dtype: float64
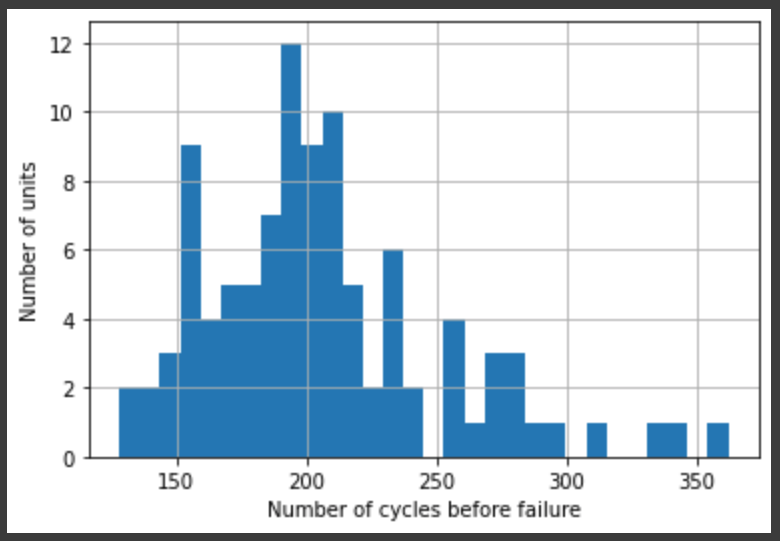
From this, we can infer that the remaining useful life (RUL) of each unit in the training data is time_in_cycles.max() minus the current time in cycles, for any given cycle. Let\’s add that as our dependent variable. (For the testing data, the RUL is in a separate file.)
We can check to make sure the RUL looks like we would expect:

Model Construction & Training
Model: "sequential_3" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= normalization_3 (Normalizati (None, None, 14) 29 _________________________________________________________________ lstm_3 (LSTM) (None, 32) 6016 _________________________________________________________________ dense_3 (Dense) (None, 1) 33 _________________________________________________________________ lambda_3 (Lambda) (None, 1) 0 ================================================================= Total params: 6,078 Trainable params: 6,049 Non-trainable params: 29
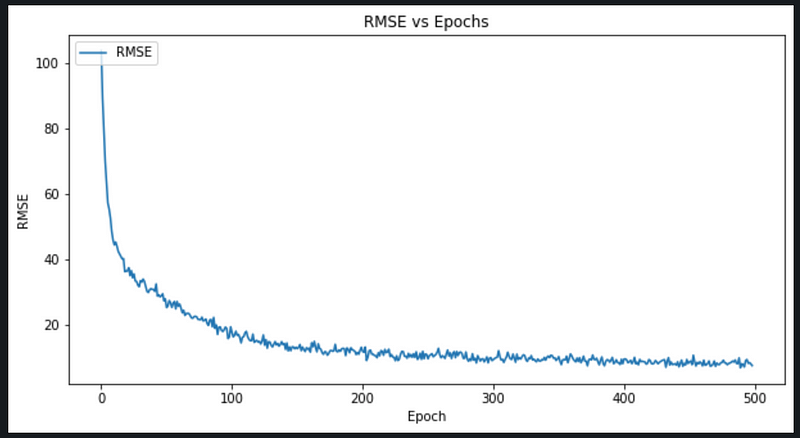
Epoch 1/499 10/10 [==============================] - 0s 6ms/step - loss: 10796.3320 - root_mean_squared_error: 103.9054 Epoch 2/499 10/10 [==============================] - 0s 6ms/step - loss: 7954.4033 - root_mean_squared_error: 89.1875 Epoch 3/499 10/10 [==============================] - 0s 6ms/step - loss: 6400.0864 - root_mean_squared_error: 80.0005 Epoch 4/499 10/10 [==============================] - 0s 4ms/step - loss: 4885.1406 - root_mean_squared_error: 69.8938 Epoch 5/499 10/10 [==============================] - 0s 4ms/step - loss: 4010.2659 - root_mean_squared_error: 63.3267 Epoch 6/499 10/10 [==============================] - 0s 4ms/step - loss: 3276.9802 - root_mean_squared_error: 57.2449 Epoch 7/499 10/10 [==============================] - 0s 4ms/step - loss: 3066.4707 - root_mean_squared_error: 55.3757 Epoch 8/499 10/10 [==============================] - 0s 4ms/step - loss: 2769.1394 - root_mean_squared_error: 52.6226 Epoch 9/499 10/10 [==============================] - 0s 4ms/step - loss: 2351.2549 - root_mean_squared_error: 48.4897 Epoch 10/499 10/10 [==============================] - 0s 4ms/step - loss: 2101.9841 - root_mean_squared_error: 45.8474 Epoch 11/499 10/10 [==============================] - 0s 4ms/step - loss: 1967.6283 - root_mean_squared_error: 44.3580 Epoch 12/499 10/10 [==============================] - 0s 4ms/step - loss: 2045.3716 - root_mean_squared_error: 45.2258 Epoch 13/499 10/10 [==============================] - 0s 4ms/step - loss: 1932.9287 - root_mean_squared_error: 43.9651 Epoch 14/499 10/10 [==============================] - 0s 4ms/step - loss: 1792.9589 - root_mean_squared_error: 42.3433 . . . . Epoch 491/499 10/10 [==============================] - 0s 4ms/step - loss: 62.6952 - root_mean_squared_error: 7.9180 Epoch 492/499 10/10 [==============================] - 0s 4ms/step - loss: 58.7008 - root_mean_squared_error: 7.6616 Epoch 493/499 10/10 [==============================] - 0s 4ms/step - loss: 48.0873 - root_mean_squared_error: 6.9345 Epoch 494/499 10/10 [==============================] - 0s 4ms/step - loss: 78.2315 - root_mean_squared_error: 8.8449 Epoch 495/499 10/10 [==============================] - 0s 4ms/step - loss: 84.7828 - root_mean_squared_error: 9.2078 Epoch 496/499 10/10 [==============================] - 0s 4ms/step - loss: 64.7266 - root_mean_squared_error: 8.0453 Epoch 497/499 10/10 [==============================] - 0s 4ms/step - loss: 68.3690 - root_mean_squared_error: 8.2686 Epoch 498/499 10/10 [==============================] - 0s 4ms/step - loss: 61.5877 - root_mean_squared_error: 7.8478 Epoch 499/499 10/10 [==============================] - 0s 4ms/step - loss: 53.9489 - root_mean_squared_error: 7.3450
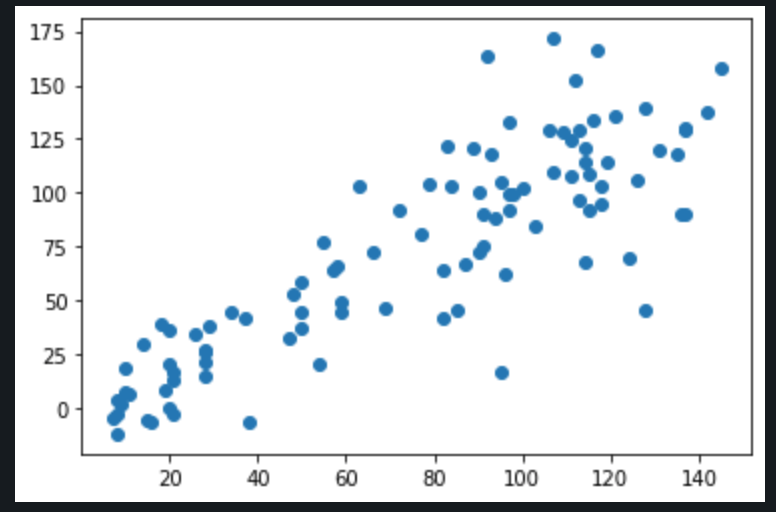
Evaluation
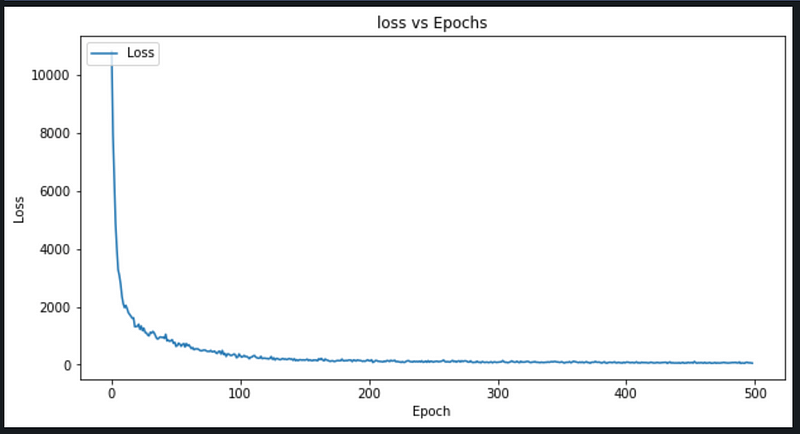
Conclusion
The model created is able to predict RUL with RMSE ~7.
Platform: cAInvas
Code: Here
Written By: Dheeraj Perumandla
Also Read: Handwritten Optical Character Recognition Calculator using CNN and Deep Learning
